게임에서 대부분의 모델링은 무수히 많은 삼각형들로 이루어져 있다.
그래서 이번에는 빛과 삼각형이 만날 때 처리를 하기 위해서 선과 삼각형의 충돌에 대해 알아볼 것이다.
삼각형은 세개의 정점으로 이루어져 있다. 당연히 이 세개의 정점은 같은 평면 위에 있을 것이고
이 때 평면의 법선벡터 n과 충돌점 p를 구하는 법을 알아보자.
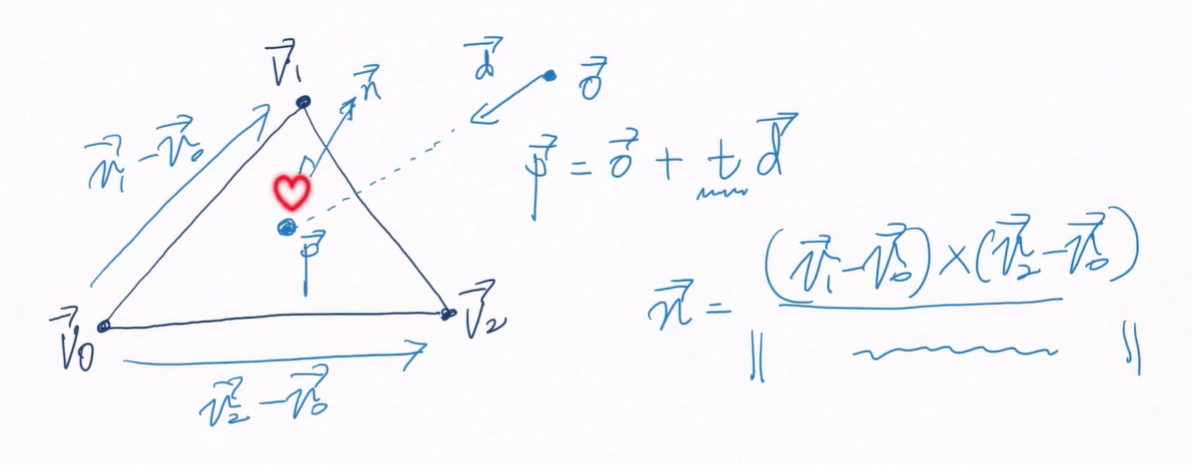
평면의 법선벡터는 v1-v0과 v2-v0을 외적하고 normalize 해주면 구할 수 있다.
여기서 주의사항은 정점의 순서에 따라 평면의 법선벡터 방향이 반대가 될 수 있다는 것이다.
예를 들어 v0, v1, v2 시계방향이라면 법선 벡터는 평면 위쪽을 가리킬 것이지만, v0, v2, v1 반시계 방향이라면 벡터는 평면 아래쪽으로 향할 것이다. 그래서 외적하는 순서에 따라 법선벡터의 방향이 바뀔 수 있으니 주의해야 한다.

평면의 법선벡터를 구했으면 충돌점도 구할 수 있다. 먼저 p - v0은 평면위의 벡터이므로 n과 내적하면 0이다.
그리고 p = o + td이므로 p에 o + td를 대입하면 최종적으로 t에 대해 위와 같은 식을 도출해낼 수 있다.
그러면 t를 구했고 o(직선 시작점), d(직선의 방향벡터)는 알고 있으므로 p(충돌점)를 구할 수 있다.
t를 구하면 t가 0보다 작을 경우 직선의 시작점 이전에 충돌한 것이므로 계산을 안해줘도 된다.
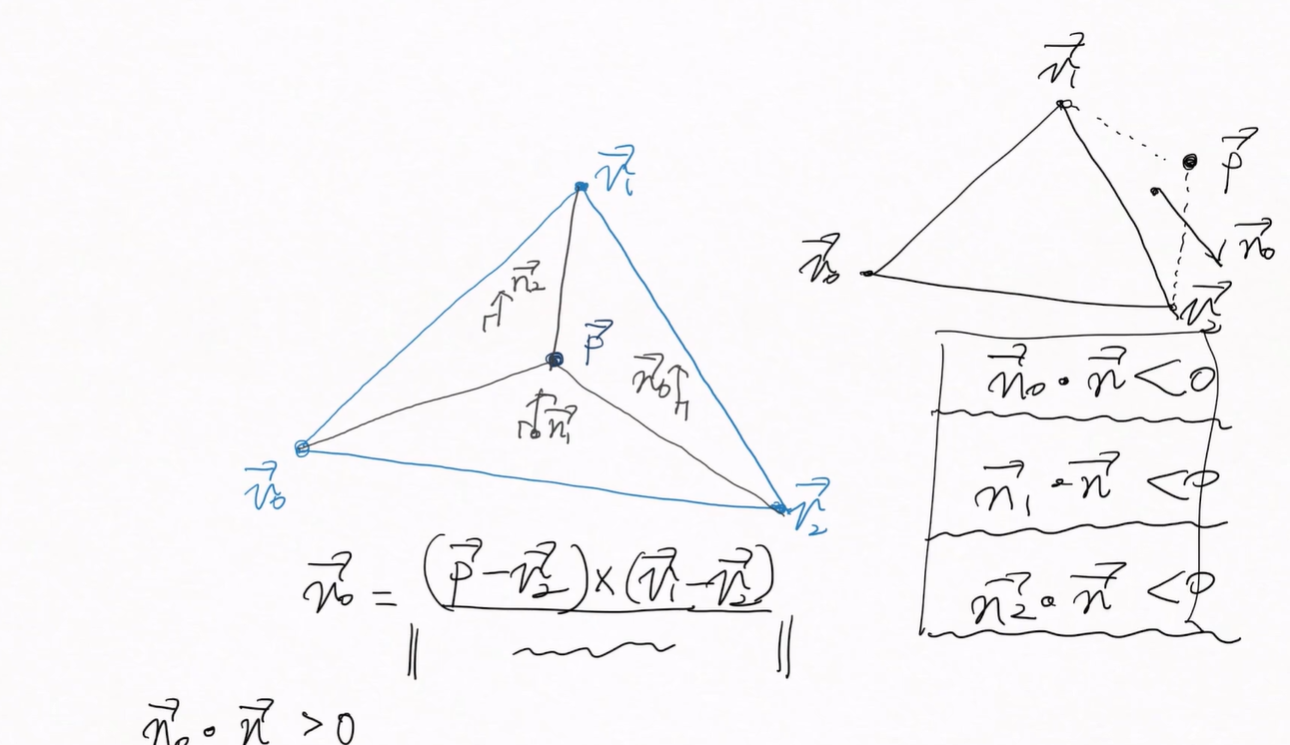
그 다음은 점이 삼각형 위에 있는지를 체크해보자. p - v2와 v1- v2를 외적했을 때 둘은 같은 평면 위에 있으므로
외적한 벡터는 평면의 법선벡터와 같을 것이다. 이렇게 세 정점과 p를 외적한 값이 각각 n0,n1,n2라고 할 때,
이들과 삼각형 평면의 법선벡터 n을 외적하면 0보다 크다. 하지만 p가 삼각형 위에 있다면 그 값은 0보다 작다.
n0,n1,n2와 n을 내적한 값이 하나라도 0보다 작다면 p는 삼각형 위에 있지 않다는 것이다.
'그래픽스' 카테고리의 다른 글
| [그래픽스] Texturing, Sampling (0) | 2023.05.17 |
|---|---|
| [그래픽스] 무게중심 좌표계 (0) | 2023.05.16 |
| [그래픽스] 선과 구의 충돌 (0) | 2023.05.11 |
| [그래픽스] Kernel, Convolution, Gaussian Blur (0) | 2023.05.10 |
| [DX12] Animation (0) | 2022.08.01 |



