오일러 각도를 이용해 회전을 하면 짐벌 락 현상이 발생한다.
오일러 각도를 이용할 때 세 축은 회전할 때 서로 종속적인데,
회전을 할 때 특정 상황에서 세 축 중 두 축이 겹쳐버리는 문제가 발생한다.
짐벌 락이 발생하면 세 축중 한 축이 소실되어버린다.
쿼터니언을 이용하면 하나의 회전축을 이용한 회전 각도를 표현할 수 있기 때문에 짐벌락 현상을 해결할 수 있다.
3차원 회전을 숫자 4개로 표현하는데 절대값이 1이라는 제약 조건이 있기 때문에 3자유도(DOF)가 있다.
벡터 v를 회전축 n에 대해 θ각도 만큼 회전 시키고 싶다면?
1.벡터에 0을 붙여 (v,0) 형태의 쿼터니언 p를 만든다.
2.회전을 표현하는 (n sin(θ/2) , cos(θ/2)) 형태의 쿼터니언 q를 만든다.
3.q의 켤레 쿼터니언 q' = (-n sin(θ/2) , cos(θ/2))을 만든다.
4.회전이 적용된 쿼터니언 p' = q*p*q' 를 구한다.
또한 회전을 표현하는 쿼터니언 q를 행렬로 만들어 곱할 수도 있다.
반대로 회전 행렬을 쿼터니언으로 만드는 것도 가능하다.
쿼터니언은 xi + yj + zk + w 로 복소수(허수) 3개와 실수 1개로 표현한다.
허수부와 실수부를 나누어 (u,w)로 표현하기도 한다.
i^2 = j^2 = k^2 = ijk = -1
ij = k = -ji
jk = i = -kj
ki = j = -ik

위는 복소수로 회전을 표현할 수 있다는 것을 설명하기 위한 그림이다.
x축을 실수부 , y축을 허수부라고 했을 때 p = 2+i에서 i를 곱할 때마다 90도씩 회전하는 것을 볼 수 있다.
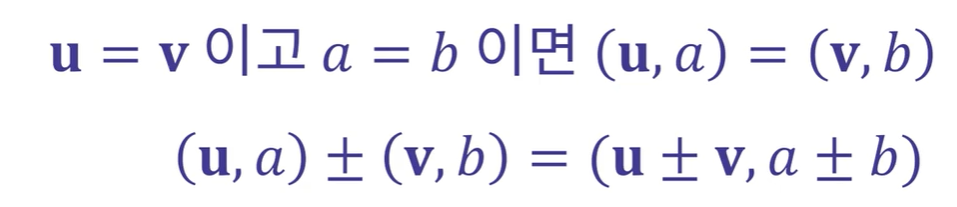




'그래픽스' 카테고리의 다른 글
| [그래픽스] Geometry Shader (0) | 2023.07.19 |
|---|---|
| [그래픽스] 쿼터니언(실습) (0) | 2023.07.19 |
| [그래픽스] Picking (렌더타겟 2개 이용, GPU->CPU로 데이터 복사) (0) | 2023.07.19 |
| [그래픽스] 후처리 - 이미지 필터 (0) | 2023.07.19 |
| [그래픽스] Texturing (0) | 2023.07.18 |
