지금까지 3차원의 물체를 2차원 좌표로 변환하기 위해 z 좌표를 없애버렸다.
이것을 Orthographic Projection(직교 투영)라고 하는데 이러면 원근감을 표현할 수 없다.
원근감을 표현하기 위해서는 Perspective Projection(원근 투영)을 이용해야 한다.

화면을 90도 돌려서 옆으로 봤을 때 그림이다. 원근감을 표현하기 위해 시점과 정점을 이었을 때
그 선 과 화면이 만나는 점에 해당 정점을 그리게 된다. 화면에 찍히는 정점의 좌표는 z축은 0,
x와 y좌표는 비례를 이용해 위 그림의 식을 이용해 구할 수 있다.
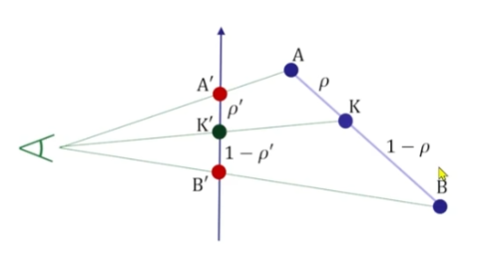
그런데 그냥 이렇게만 좌표를 구하면 정점 내부의 픽셀들이 정상적으로 보이지 않는데, 현재는
정점 내부 픽셀을 무게 중심 좌표계를 이용해서 표현하는데, 3차원의 물체에서 표현하는게 아니라
2차원에서 무게중심 좌표계를 사용하기 때문이다. 직교 투영을 제외했을 때 p와 p'가 다르기 때문에
실제 길이는 p인데 p'에 대해 계산하므로 이를 보정해줘야 할 필요가 있다.

그래서 이것을 보정한식이다. w0, w1, w2가 무게 중심 좌표계에서 각 정점에 대한 비율이고 제타는 시점에서부터 각 정점까지의 거리이다. 그랬을 때 w0', w1', w2'를 다시 구해서 계산해주면 된다.
'그래픽스' 카테고리의 다른 글
| [그래픽스] Row-Major vs Column-Major (0) | 2023.05.30 |
|---|---|
| [그래픽스] Blinn Phong으로 lighting 계산하기(halfway vector) (0) | 2023.05.29 |
| [그래픽스] 쉐이더(Shader) 개념 (0) | 2023.05.28 |
| [그래픽스] 래스터화(Rasterization)가 빠른 이유 (0) | 2023.05.23 |
| [그래픽스] 투명한 물체에서 빛의 굴절 (0) | 2023.05.18 |


