DP 문제를 풀기 시작하면서 막 시작하니 감이 잘 안 와서
루키스 알고리즘 강의를 보면서 DP 문제를 푸는 법을 정리해보려고 한다.
n개중에 r개를 뽑는 경우의 수를 nCr이라고 할 때
nCr = n-1Cr-1 + n-1Cr 이다. 예시를 들어보겠다.
5개 중에 2개의 공을 뽑는다고 하자. 그리고 무작위 공 하나를 선택하면 공 4개가 남는다.
선택한 공을 뽑는다면 나머지 공 4개중 하나를 뽑을 것이고
선택한 공을 뽑지 않는다면 나머지 공 4개중 두 개를 뽑을 것이다.
그러므로 5C2 = 4C1 + 4C2이다. 이것을 이제 코드로 표현해보자.
int combination(int n, int r)
{
if(r==0 || n==r)
return 1;
return combination(n-1,r-1) + combination(n-1,r);
}r이 0일 때(0개를 뽑을 때)와 n과 r이 같을 때(모두 뽑을 때) 조합 값이 1인 것을 제외하면
모든 경우에서 return combination(n-1,r-1) + combination(n-1,r); 이 구문을 따른다.
이 코드만 보면 그냥 재귀로 해결할 수 있는데, 문제는 실행 시간이 너무 오래 걸린다. 계산을 중복해서 하기 때문이다.
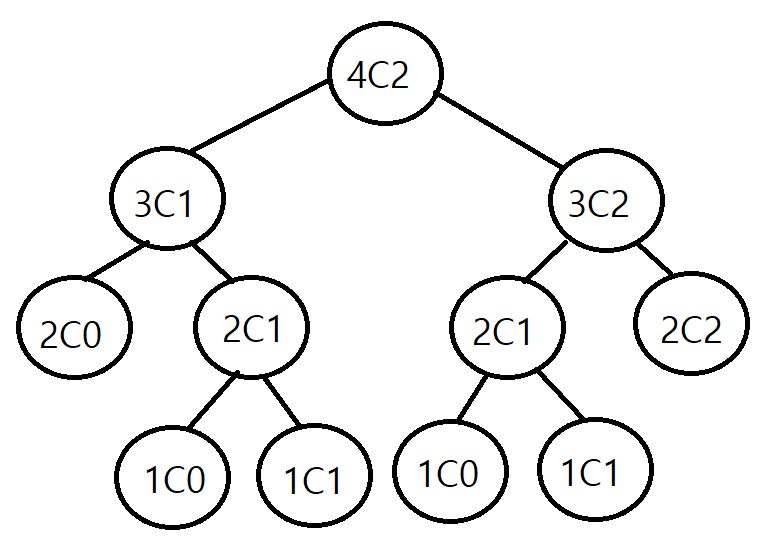
4C2를 재귀로 계산할 때 이렇게 진행되는데, 1C0,1C1,2C1이 두번씩 계산되고 있다. 4C2같은 작은 계산에도 이렇게
중복이 발생하는데 숫자가 커질수록 중복되는 계산은 기하급수적으로 증가한다.
동적 계획법을 이용하면 계산할 때 그 값을 저장하고 이미 계산된 값이라면 스킵해서 효율적으로 처리한다.
int combination(int n, int r)
{
if(r==0 || n==r)
return 1;
if(cache[n][r] != -1)
return cache[n][r];
return cache[n][r] = combination(n-1,r-1) + combination(n-1,r);
}cache를 처음에 -1로 초기화하고 계산한 값을 cache에 저장한다.
cache에 이미 값이 저장되어 있다면 재귀를 진행하지 않고 저장한 값을 반환한다.
일반 재귀 코드는 350ms가 넘게 시간이 걸리는데 DP는 0ms로 순식간에 계산이 끝난다.
DP를 사용하면 일반 재귀에 비해 성능 개선 효과가 어마어마하게 있는 것을 알 수 있다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 동적 계획법(DP) - TIC-TAE-TOE(3목) (0) | 2023.02.23 |
|---|---|
| [알고리즘] 동적 계획법(DP) - LIS(Longest Increasing Subsequence) (0) | 2023.02.22 |
| [알고리즘] 벨만 포드 알고리즘 (0) | 2023.02.20 |
| [알고리즘] BFS, DFS 언제 사용할까? (0) | 2023.02.13 |
| [알고리즘] 그래프와 트리 (트리는 방향 그래프인가?) (0) | 2023.02.09 |