

부동 소수점은 컴퓨터가 실수를 저장하는 방식이다.
부호: 부호는 0이 양수, 1이 음수이다.
지수부: 위에서는 직관적인 이해를 위해 10의 거듭제곱을 곱하는데 실제로는 2의 거듭제곱으로 지수를 표현한다.
지수를 n이라고 했을 때 가수부에 2^n이 곱해지고 음수 지수도 표현해야 하므로 부호를 가져야 한다.
부호파트는 따로 쓰지 않고 127의 바이어스를 적용해 0~255까지의 범위를 가지는 지수에 127씩 빼준다.
가수부: 같은 수를 표현하는 방법이 여럿 존재하면 두 변수의 상등 비교 연산을 하기 까다롭기 때문에
가수의 정수부를 한자리로 제한하는 정규화를 한다. (ex 1.2345 ,1.23)
가수도 1~2 사이의 수로 제한되어 항상 1.~~의 형태를 띄게 된다. (마찬가지로 정규화 규칙)
그래서 규칙때문에 제일 왼쪽 비트는 항상 1이라고 가정해 저장하지 않고 정밀도가 2배 더 높아진다.
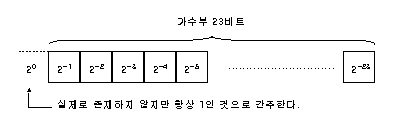
가수부는 왼쪽 비트부터 1/2, 1/4, 1/8...씩 가중치를 가지며 2^0은 1로 간주하므로
1에 가중치들을 더하면 실제 가수가 된다.
0 01111101 10000000000000000000000
이 실수가 어떤 수인지 계산해보자. 먼저 부호가 0이므로 양수이다.
가수는 맨왼쪽 비트만 1이므로 1 + 1/2 = 3/2이다.
지수는 계산하면 125이므로 바이어스 127을 뺴면 -2이다.
답은 (3/2)*2^-2 = 3/8 = 0.375이다.
'C++' 카테고리의 다른 글
| [C++] 매개변수로 이중포인터를 사용해야 할 경우 (0) | 2023.02.01 |
|---|---|
| [C++] 우선 순위 큐 정렬 방법 변경 (0) | 2023.01.31 |
| [C++] 포인터 비트 단위 이해 (0) | 2022.12.25 |
| [C++] 전역 변수, 정적 변수, 외부 변수 (0) | 2022.12.23 |
| [C++] 람다 (0) | 2022.06.25 |
