힙 정렬
힙 정렬은 힙의 특성을 이용한 정렬이다.
우선순위 큐가 힙의 특성을 이용하기 때문에 우선순위 큐를 사용하여 구현할 수 있다.
void HeapSort(vector<int>& v)
{
priority_queue<int, vector<int>, greater<int>> pq;
// O(NlogN)
for (int num : v)
pq.push(num);
v.clear();
// O(NlogN)
while (pq.empty() == false)
{
v.push_back(pq.top());
pq.pop();
}
}우선순위 큐에 push할 때 시간복잡도는 logN이고 그걸 N번 반복하므로 시간복잡도는 NlogN이다.
pop하는 것도 logN이고 우선순위큐가 비워질 때까지 N번 반복하브로 마찬가지로 NlogN이다.
병합정렬
병합정렬은 분할 정복을 이용하는데 분할, 정복, 결합 세 순서로 나누어진다.
문제를 더 단순한 문제로 분할, 분할한 문제를 정복, 그리고 결과를 결합한다.
void MergeResult(vector<int>& v, int left, int mid, int right)
{
// [2][3][7][K][4][8][9][J]
// [l] [r]
int leftIdx = left;
int rightIdx = mid + 1;
// [2]
vector<int> temp;
while (leftIdx <= mid && rightIdx <= right)
{
if (v[leftIdx] <= v[rightIdx])
{
temp.push_back(v[leftIdx]);
leftIdx++;
}
else
{
temp.push_back(v[rightIdx]);
rightIdx++;
}
}
// 왼쪽이 먼저 끝났으면, 오른쪽 나머지 데이터 복사
if (leftIdx > mid)
{
while (rightIdx <= right)
{
temp.push_back(v[rightIdx]);
rightIdx++;
}
}
// 오른쪽이 먼저 끝났으면, 왼쪽 나머지 데이터 복사
else
{
while (leftIdx <= mid)
{
temp.push_back(v[leftIdx]);
leftIdx++;
}
}
for (int i = 0; i < temp.size(); i++)
v[left + i] = temp[i];
}위 코드는 vector v를 반으로 나누어 왼쪽 절반, 오른쪽 절반을 index에 따라 비교해서 더 작은 값을 push한다.
그러면 둘 중 한 쪽의 index가 먼저 범위 밖으로 나오는데, 그러면 나머지 다른쪽 벡터를 temp에 push한다.
void MergeSort(vector<int>& v, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) / 2;
MergeSort(v, left, mid);
MergeSort(v, mid + 1, right);
MergeResult(v, left, mid, right);
}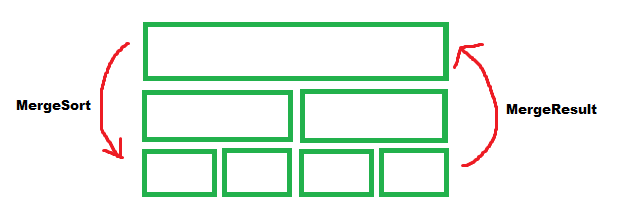
MergeSort로 위에서 밑으로 분할하고 MergeResult로 결합하면서 다시 한단계씩 위로 올라간다.
병합 정렬의 시간복잡도는 NlogN이다.
'알고리즘' 카테고리의 다른 글
| [알고리즘] 상호 배타적 집합 (Disjoint set), 유니온 파인드 (Union find) (0) | 2022.07.11 |
|---|---|
| [알고리즘] 해시 테이블 (0) | 2022.07.11 |
| [알고리즘] 레드 블랙 트리 - 2.삭제 (0) | 2022.07.10 |
| [알고리즘] 레드 블랙 트리 - 1.삽입 (0) | 2022.07.09 |
| [알고리즘] 이진 탐색 트리 (Binary Search Tree) (0) | 2022.07.05 |

