카메라 기준으로 좌표가 바뀌기 때문에 좌표계의 변환은 수시로 일어난다. 그래서 새로운 좌표계를 기준으로 행렬을 변환하는 것은 중요하다. 예시로 아래 그림의 좌표 M을 A좌표계에서 B좌표계로 변환해서 표현해보겠다.
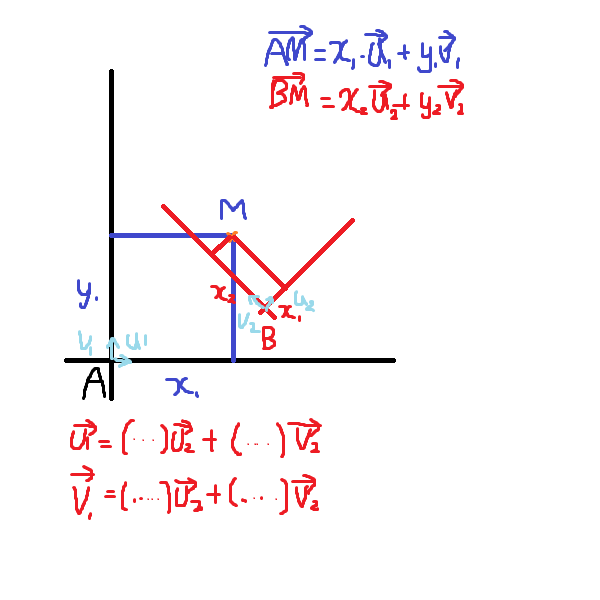
1.벡터 AM을 AB+BM으로 나눈다.
2.AB를 넘기고 BM을 그림처럼 (...)u2 + (...)v2 형식으로 표현한다.
식을 행렬로 표현하면
(x,y,z,1)와 Ux Uy Uz 0 를 곱한 것이 된다.
Vx Vy Vz 0
Wx Wy Wz 0
Qx Qy Qz 1
X = xUx + yUy + zUz ,
Y = xVx + yVy + zVz ,
Z = xWx + yWy + zWz 는 A좌표를 B좌표계 기준으로 표현한 것이다.
만약 위치벡터가 아닌 기하벡터(방향벡터)라면 시작점이 존재하지 않기 때문에 행렬의 가장 밑 줄, translation 성분(qx,qy, qz)은 사라진다. 행렬식을 적용할 때 변화하는 대상이 위치(좌표)라면 (x,y,z,1)로 계산하고 방향(벡터)라면 (x,y,z,0)으로 계산한다.
'그래픽스' 카테고리의 다른 글
| [DX12] Normal Mapping (0) | 2022.02.28 |
|---|---|
| [DX12] Projection, Screen 변환 행렬 (0) | 2022.02.26 |
| [DX12] World, View 변환 행렬 (0) | 2022.02.26 |
| [DX12] 삼각형 그리기 (0) | 2022.02.24 |
| [DX12] 장치 초기화 개요 (0) | 2022.02.20 |

